今天在写数据结构实验的时候，一不小心选到了图论单元应该最难的实验：中国邮递员问题（绝对不是因为题目太短以为很简单所以才选的QAQ）由于题目过于简短，不太容易上手，所以我选择查阅资料学习后再完成。偏偏在各个地方都不太容易找到这个问题的完整求解方法，故博主学习整理之后，将学习的心路历程分享出来，希望能帮助到遇到困难的朋友。

1. 问题描述

在一座城市有一个邮局，邮局的快递员每天在城市不同的区域派送邮件，区域与区域之间有街道相连。快递员希望在派件的时候：

• 经过所有区域与区域之间的街道至少一次
• 派件结束后回到邮局
• 整个路程最短

请输出符合上述条件的路线。

中国邮递员问题（CPP）由管梅谷教授于1960年提出，将这个问题抽象为图论可以理解为：在一张带非负权连通图上遍历所有的边，最后回到遍历起点，要求总权最小求遍历路径。其中区域可以抽象成顶点，街道可以抽象为边，所管辖的城市可用一个赋权图来表示，其中边的权重表示对应街道的长度。

对于这个问题已经证明：

• 如果只含有双向道（无向图），为P问题。
• 如果只含有单向道（有向图），为NPC问题。
• 如果既含有双向道，又含有单向道，为NP-Hard问题。

本文在实际生活场景下讨论无向图的CPP。

2. 问题分析

从题目可以很容易看出，既要经过所有的边，又要最短，那最优的情况的就是每条边只走一次，即一笔画。围绕这个特点我们可以知道，如果所给图为欧拉图，那么存在欧拉回路使得每条边都只遍历一次且能回到起点，在这种情况下欧拉回路就是最优环游。

所以可以将这个问题分成两类：

• 所给图为欧拉图，求出欧拉回路。
• 所给图为非欧拉图。

2. 1 欧拉图

对于求解欧拉回路有两种解法：Fleury和Hierholzer，不过Hierholzer的效率更高，在这里介绍下Hierholzer算法求解欧拉回路。

Hierholzer算法的核心很简单，就是通过不断删边找到可能的欧拉回路。算法步骤为：

• 从当前点开始，遍历关联边对应的相邻点，并将这条关联边删除。
• 若当前点没有关联边，则将当前点压入序列栈中。

我们用一个简单的例子来直观的理解这个算法的思路：

一个简单的示例

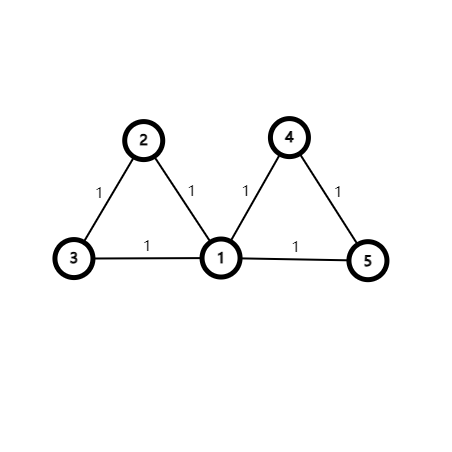
在上图中，比较容易知道所有的顶点的度都为偶数，存在一条欧拉回路，使得能够一次性遍历所有的边，符合Hierholzer算法的应用条件，我们选取顶点1为邮局的位置（起点）：

1. 对1的所有关联边进行遍历，其相邻点有：2,3,4,5
2. 选取1的相邻点2，1-2没有被访问过，访问1-2
3. 对2的所有关联边进行遍历，其相邻点有：1,3
4. 选取2的相邻点1，2-1已经被访问过，不再访问
5. 选取2的相邻点3，2-3没有被访问过，访问2-3
6. 对3的所有关联边进行遍历，其相邻点都有：1,2
7. 选取3的相邻点1，3-1没有被访问过，访问3-1
8. 对1的所有关联边进行遍历，其相邻点有：2,3,4,5
9. 选取1的相邻点2,3，1-2和1-3都被访问过，不再访问
10. 选取1的相邻点4，1-4没有被访问过，访问1-4
11. 对4的所有关联边进行遍历，其相邻点有：1,5
12. 选取4的相邻点1，4-1已经被访问过，不再访问
13. 选取

代码如下：

struct info
{
    int to,dis;
};
std::vector<info> g[55];
std::stack<int> path;
bool vis[55][55]；
void Hierholzer(int now)
{
    for(info i:g[now])
        if(!vis[now][i.to]){
            vis[now][i.to]=true;
            vis[i.to][now]=true;
            Hierholzer(i.to);
        }
    path.push(now);
}

在上述代码中：

• info为顶点的相关信息，to表示与当前顶点相连的下一个顶点的编号，dis表示当前节点到下一个结点的距离（其实也可以用std::pair来实现，不过我觉得定义一个新的结构体比较直观一点）
• g[now]为std::vector类型的邻接表，用于存储当前节点相连的下一个节点的info
• path为用于存储最终的欧拉回路路径
• vis[now][i.to]用于判断当前边是否有被访问过，由于是无向图，所以往返路径都要标记为已访问

由于欧拉回路能一次性遍历所有边，故当访问到当前顶点没有关联边的时候，其在路径中的位置也就随之确定。